Surfaces minimales
Quand on découpe un trou dans une surface et qu'on le remplace par un film d'eau savonneuse, ce film se tend pour occuper une aire aussi petite que possible.
Si la surface avait exactement la forme qu'a prise le film, et que cela est vrai pour tout découpage, on dit qu'elle est minimale : c'est donc une surface qui minimise l'aire autour de chacun de ses points.
On peut y penser comme une membrane de latex tendue, la pression de l'air étant la même de chaque côté de cette membrane.
Les surfaces minimales peuvent aussi être caractérisées en termes de courbure : ce sont celles de courbure moyenne nulle ; contrairement à une sphère, qui est de courbure positive, elles ont en chaque point l'apparence d'une selle de cheval courbée dans des sens opposés le long de deux directions perpendiculaires :
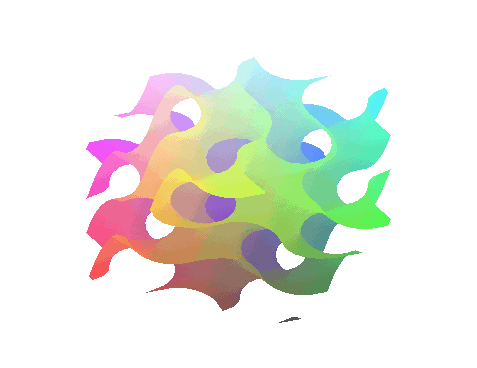
La courbure, et donc l'équation de surface minimale, fait intervenir l'opérateur Laplacien :
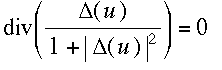
Lors de ses études sur la capillarité et la loi de pression, Laplace avait exprimé que la différence de pression entre les deux faces d'une paroi élastique est proportionnelle à sa courbure. C'est ainsi qu'un ballon gonflé prend une forme à courbure positive, alors qu'un film de plastique alimentaire maintenant un saladier "sous vide" se creuse au milieu.
Pour en savoir beaucoup plus, consultez ce site complet dédié aux surfaces minimales.
Retour à la page principale