Laplace transformé par son opérateur

Si une fonction f vérifie l'équation de Laplace Delta(f)=0, ses moyennes sur deux cercles concentriques sont égales :
pour tout r, int_D(r) f =int_D(r') f.

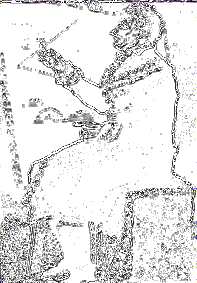
Sur une photo, les contours sont des points où la fonction f(x)="luminosité au point x" a un laplacien Delta(f)(x) très grand, ce qui se voit en calculant la différence g(x) des moyennes de f sur 2 cercles concentriques en x. Le graphique dont la luminosité en x est g(x) est donc noir sauf sur les contours. Son négatif forme donc un dessin au trait noir sur fond blanc, comme dans les exemples ci-dessous.

Pour en savoir plus sur l'équation de Laplace, voir ce cours concis , ainsi que ces renseignements

Une collection de "transformés de Laplace" par lui-même

----->
Laplacien discret